Vektoren
Vektoren haben eine Länge und eine Richtung (Richtungsvektoren). Meistens geht es aber um Ortsvektoren, die zusätzlich noch einen festen Ort haben und vom Ursprungspunkt $(0, 0)$ ausgehen. Vektoren werden als fettgedruckte Kleinbuchstaben $\boldsymbol{a}$ oder mit einem Pfeil $\vec{a}$ dargestellt.
Gegeben seien die Vektoren:
$$ \vec{a} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} \quad\quad \vec{b} = \begin{bmatrix} 5 \\ 6 \\ 7 \\ 8 \end{bmatrix} $$
Vektoraddition
Die Vektoren werden komponentenweise miteinander addiert.
$$ a + b = (6, 8, 10, 12) $$
Skalare Multiplikation
Die skalare Multiplikation skaliert den Vektor, ein skalar ist für gewöhnlich eine reelle Zahl wie zB 2 oder 3.
$$ 5 * a = (5, 10, 15, 20) $$
$$ 2 * b = (10, 12, 14, 16) $$
Rechenregeln
Vektoren haben dieselben Rechenregeln die wir auch schon von den Grundrechnungsarten her kennen:
- Kommutativgesetz: $a + b = b + a$
- Distributivgesetz: $\lambda \cdot (a + b) = \lambda a + \lambda b$
- Assoziativgesetz: $a + (b + c) = (a + b) + c$
Übungsbeispiel 3
Geben Sie alle Lösungen der Gleichung $4x + 2y = 0$ an.
Tipp: Versuchen Sie eine Lösung durch Probieren zu finden $x = a, y = b$. Zeigen Sie dann, dass alle Vielfachen $x = c \cdot a, y = c \cdot b$ auch Lösungen sind.
Lösung
Die Gleichung kann als Skalarprodukt betrachtet werden:
$$\vec{v} = (x,y) \quad \vec{n} = (4,2)$$
$$\vec{n} \cdot \vec{v} = 4x + 2y = 0$$
Das bedeutet, dass der Vektor $\vec{v}$ senkrecht orthogonal zu $\vec{n}$ sein muss.
$$(4,2) \cdot (-2,4) = 4(-2) + 2(4) = -8 + 8 = 0$$
Übungsbeispiel 6
Geben Sie alle Lösungen der Gleichung $x + 2y + z = 0$ an.
Tipp: Setzen Sie eine Variable 0 und gehen Sie wie bei Aufgabe 3 vor. Der Lösungsraum hat die Form $\mathbb{R} a + \mathbb{R} b$
Lösung
1. x auf 0 setzen
\begin{align*}
2y + z & = 0 \\
z & = -2y \\
(x, y, z) & = (0, y, -2y)
\end{align*}
2. y auf 0 setzen
\begin{align*}
x + z & = 0 \\
z & = -x \\
(x, y, z) & = (x, 0, -x)
\end{align*}
3. Als Linearkombinationen betrachtet
$(x, y, z) = a \cdot (0, 1, -2) + b \cdot (1, 0, -1)$
Nullvektor
Der Nullvektor $\vec{0}$ hat keine Länge und keine Richtung. Der Nullvektor ist sozusagen das neutrale Element der Vektoraddition.
$$\vec{0} = 0 \cdot \vec{a}$$
$$\vec{a} + \vec{0} = \vec{a}$$
Punkt vs. Vektor
Es gibt eigentlich nur 2 sinnvolle Operationen mit denen man Punkte und Vektoren zusammen bringen kann:
- Punkt + Vektor: verschiebt den Punkt um den Vektor
- Punkt - Punkt: ergibt einen Richtungsvektor
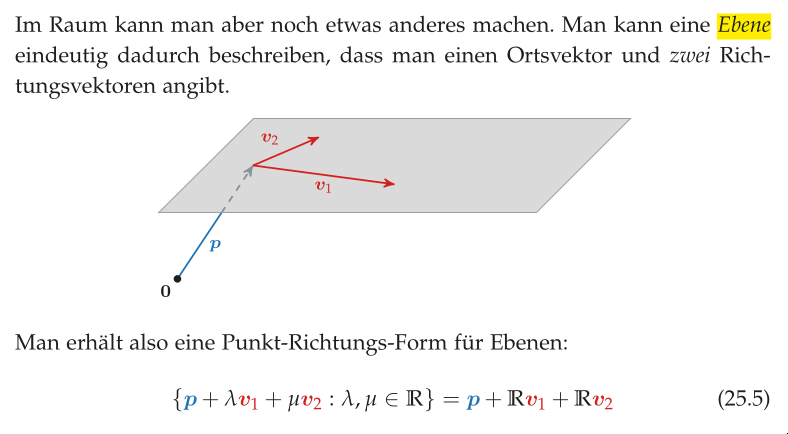
Die Punkt-Richtungs-Form
Man kann eine Gerade $g$ durch eine Menge von Punkten darstellen, indem man zu einem Punkt einen Richtungsvektor dazu addiert. Je nachdem mit welchem Skalar man diesen Richtungsvektor multipliziert, erhält man einen anderen Punkt auf dieser Geraden. Die Punkt-Richtungs-Form schaut allgemein (links) und konkret fur einen Punkt (rechts) geschrieben so aus:
$$g = \{p + \lambda \mathbb{R}\} \quad\quad g = \{p + \lambda \cdot \vec{v} \mid \lambda \in \mathbb{R}\}$$
Es gibt auch eine alternative Form der Geradendarstellung die man durch Umformen erreicht:
$$g = \{\lambda p_1 + \mu p_2\ \mid \lambda,\mu \in \mathbb{R}, \lambda + \mu = 1\}$$
Linearkombination
Das ist eine sogenannte Linearkombination: $\lambda p_1 + \mu p_2$
Affinkombination
Eine Affinkombination hingegen unterliegt noch der Bedingung, dass beide Faktoren zB eine 1 ergeben.
Übungsbeispiel 4
Geben Sie eine Punkt-Richtungsform der Geraden $g$ durch die Punkte $p_1 = (1,2)$ und $p_2 = (-3,1)$ an. Schreiben Sie die Gerade in der Form $p + \mathbb{R} \cdot \vec{v}$ an. Überprüfen Sie rechnerisch, ob der Punkt (5, 3) auf dieser Geraden liegt. Überprüfen Sie ebenfalls rechnerisch, ob er auf der Strecke zwischen $p_1$ und $p_2$ liegt.
Lösung
1. Bestimmen des Richtungsvektors $\vec{v}$
$$\vec{v} = p_2 - p_1 = (-3,1) - (1,2) = (-4,-1)$$
2. Punkt-Richtungs-Form der Geraden $g$
$$g = p_1 + \lambda \cdot \vec{v} = (1,2) + \lambda \cdot (-4, 1) \mid \lambda \in \mathbb{R}$$
$$g(\lambda) = (1 - 4\lambda) + (2 - 1\lambda)$$
3. Überprüfen ob der Punkt $(5, 3)$ auf der Geraden liegt
$$g(5) = 1 - 4\lambda\quad\quad g(3) = 2 - \lambda$$
$$5 = 1 - 4 \cdot (-1) = 1 + 4 = 5$$
Da beide Gleichungen erfüllt sind, liegt der Punkt auf der Geraden.
4. Überprüfen ob der Punkt $(5, 3)$ auf der Strecke zwischen $p_1$ und $p_2$ liegt
Da $\lambda = -1$ nicht im Intervall $[0,1]$ ist, liegt der Punkt nicht auf der Strecke zwischen $p_1$ und $p_2$.
Übungsbeispiel 5
Geben Sie die Gerade $y = 3x + 4$ in Punkt-Richtungsform an.
Tipp: Berechnen Sie zwei Punkte auf der Gerade und gehen Sie wie in Aufgabe 4 vor.
Lösung
1. Zwei beliebige Werte für $x$ auswählen
$$y = 3 \cdot 0 + 4 = 4 \quad\longrightarrow\quad p_1 = (0,4)$$
$$y = 3 \cdot 1 + 4 = 7 \quad\longrightarrow\quad p_2 = (1,7)$$
2. Die Punkt-Richtungs-Form aufstellen
$$g = p_1 \cdot \lambda + p_2 \cdot \mu = (0,4) \lambda + (1,7) \mu$$
Oder anhand der Steigung den Richtungsvektor ablesen:
$$\vec{v} = (1, 3) \quad\longrightarrow\quad g = (0,4) + \lambda \cdot (1,3)$$
Übungsbeispiel 7
Geben Sie eine Punkt-Richtungsform der Ebene an, die die 3 Punkte $p1 = (1, 2, 1)$, $p2 = (3, −1, 5)$ und $p3 = (4, 0, −6)$ enthält.
Lösung
1. Richtungsvektoren bestimmen
$$\vec{v_1} = p_2 - p_1 = (3,-1,5) - (1,2,1) = (2,-3,4)$$
$$\vec{v_2} = p3 - p_1 = (4,0,-6) - (1,2,1) = (3,-2,7)$$
2. Punkt-Richtungs-Form in der Ebene $E$ aufstellen
$$E = p_1 + \lambda \vec{v_1} + \mu \vec{v_2} = (1,2,1) + \lambda (2,-3,4) + \mu (3,-2,7)$$
Schnittmenge von geometrischen Figuren

Theoriefragen
Was bewirkt die Addition eines Orts- und Richtungsvektors?
eine Verschiebung
Was beschreibt der Ausdruck $p + \mathbb{R} \cdot \vec{v}$?
eine Gerade
Wie kann man alle Punkte auf einer Strecke zwischen zwei Punkten $p_1$ und $p_2$ angeben
durch die Affinkombination $\lambda p_1 + \mu p_2 \mid \lambda,\mu = [0,1], \lambda + \mu = 1$
Wieviel Möglichkeiten gibt es eine Gerade durch die Punkt-Richtungs-Form darzustellen?
unendlich viele